Пример седьмой. Вычисление определителя матрицы.
Из свойств определителя известно, что определитель матрицы порядка N может
быть представлен в виде суммы N определителей N-1 порядка (разложение по
строке или столбцу). Предположим мы раскладываем по первому столбцу. При этом
определитель равен сумме произведений элементов этого столбца на минор
данного элемента матрицы и на -1 в степени суммы индексов элемента.
Минор элемента а[i,j] матрицы - это определитель матрицы, полученной
вычеркиванием i-той строки и j-того столбца.
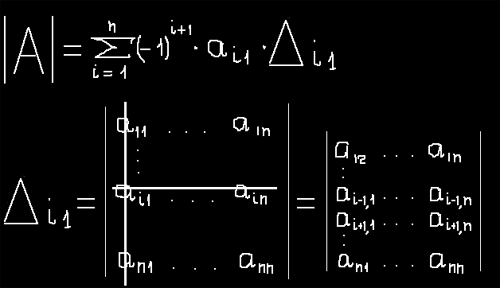
Таким образом можно воспользоваться рекурсией и написав одну простую
процедуру вычислять определители матрицы любого порядка.
const n=4; { размерность матрицы }
type matr=array[1..n,1..n] of longint;
var a,b:matr;
i,j,dt:longint;
procedure PrintMatr(m:matr;n:integer);
{ процедура вывода матрицы на экран }
var i,j:integer;
begin
for i:=1 to n do
begin
for j:=1 to n do
write(m[i,j]:3);
writeln;
end;
end;
procedure GetMatr(a:matr; var b:matr; m,i,j:integer);
{ Вычеркивание из матрицы строки и столбца }
var ki,kj,di,dj:integer;
begin
di:=0;
for ki:=1 to m-1 do
begin
if (ki=i) then di:=1;
dj:=0;
for kj:=1 to m-1 do
begin
if (kj=j) then dj:=1;
b[ki,kj]:=a[ki+di,kj+dj];
end;
end;
end;
Function Determinant(a:matr;n:integer):longint;
{ Вычисление определителя матрицы }
var i,j,d,k:longint;
b:matr;
begin
d:=0; k:=1;
if (n<1) then
begin
writeln('Determinant: Cann''t run. N=',n); halt;
end;
if (n=1)
then d:=a[1,1]
else if (n=2)
then d:=a[1,1]*a[2,2]-a[2,1]*a[1,2]
else { n>2 }
for i:=1 to n do
begin
GetMatr(a,b,n,i,1);
{writeln('i=',i,' a[',i,',1]=',a[i,1]);
PrintMatr(b,n-1);}
d:=d+k*a[i,1]*Determinant(b,n-1);
k:=-k;
end;
Determinant:=d;
end;
begin
{ Заполнение матрицы случайными числами }
randomize;
for i:=1 to n do
for j:=1 to n do
a[i,j]:=random(5);
{ Печать исходной матрицы }
PrintMatr(a,n);
{ Вычисление и вывод определителя }
dt:=Determinant(a,n);
writeln('=========');
writeln('Determinant=',dt);
end.
|

