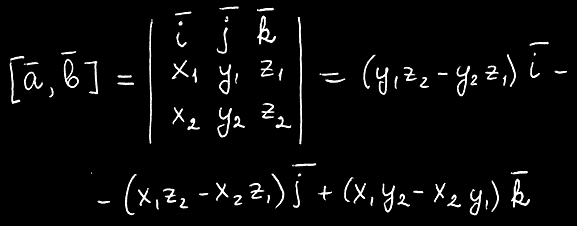Mail

В этот день много лет назад...
25 апреля. В 1547 году (477 лет назад) - Крупнейшим пожаром сжигается Москва.

Turbo Pascal Examples

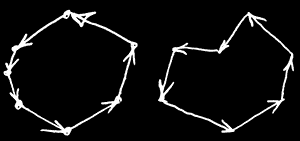
Графика:
Построение графика функции
Прыгающий по экрану мячик.
Качание маятника.
Вложенные цветные круги.
Броуновское движение. Использование объектов.
Матрицы и массивы:
Сортировка элементов массива.
Удаление одинаковых элементов.
Простой пример на поворот матрицы.
Сортировка методом Шелла. +функции измерения временных интервалов.
Проверка выпуклости многоугольника.
Перемоножение матриц
Вычисление определителя матрицы. Рекурсия.
Нахождение обратной матрицы.
Задача об автостоянке.
Рекурсия. Подземелье сокровищ.
Численные методы:
Задачка на определение угла между стрелками часов.
Проверка на принадлежность точки многоугольнику.
Нахождение точки пересечения двух отрезков на плоскости.
Сортировка методом Шелла. +функции измерения временных интервалов.
Сортировка методом "пузырька". Пример на динамические структуры данных. Связанные списки.
Нахождение корня функции методом половинного деления.
Вычисление арккосинуса
Нахождение суммы цифр натурального числа.
Работа с фалами:
Рекурсивное сканирование директорий.
Работа со строками:
Работа со словами в предложении с разделителями.
Простейший синтаксический анализатор для распознавания и вычисления многчлена.
Синтаксический анализатор для распознавания и вычисления многчлена.
Работа со строками: смена кодировки, удаление тегов из HTML текста, обработка
Переименование файлов из кириллицы в латиницу.
Выдача контекстной подсказки.
Частотный словарь символов.
Подсчет повторяющихся символов в строке.
Ссылочные переменные:
Моделирование стека.
Пасьянс "Косынка".
Игры:
Пасьянс "Косынка".
Игра "Питон"
Игра "Анацефал". Пример использования объектов.
Игра "Минное поле"
Большие проекты:
Электронная картотека (без исходника)

Проверка выпуклости многоугольника.

Задача, скорее, не на программирование, а на векторную алгебру. Итак, условие. Задан многоугольник. Требуется определить, является ли он выпуклым.
Для начала определимся, что есть выпуклый многоугольник. Многоугольник называется выпуклым, если любые две точки его периметра можно соединить отрезком, каждая точка которого лежит внутри многоугольника.

Здесь слева - выпуклый многоугольник, справа - нет. Одним из критериев выпуклости является следующий. Многоугольник будет выпуклым, если для векторов, составляющих его периметр, выполняется условие: векторные произведение соседних векторов должны иметь одинаковый знак. В общем случае, произведение векторов в трехмерном пространстве находится по формуле:

Здесь i, j, k - орты декартовой системы (вектора единичной длины, сонаправленные с осями координат).
Однако, если мы рассматриваем вектора, лежащие в одной плоскости, то для этого случая z-составляющая векторов будет нулевой. А тогда наша формула выродиться в:
[a,b]=(x₁*y₂-x₂*y₁)*k
Таким образом, мы должны обойти все пары соседних сторон-векторов и посмотреть, все ли их произведения одного знака. (То есть все ли значения разности произведений (x_i*y_i+1-x_i+1*y_i) одного знака для всех i от 1 до N-1).
Итак алгоритм:

Задаем N - количество вершин многоугольника
Задаем (вводим или присваиваем) все вершины многоугольника P^x_i, P^y_i для всех i от 1 до N.
Полагаем многоугольник выпуклым Q=true.
Вычисляем T=x_N*y₁-x₁*y_N
Вычисляем Z=T/|T|, |T| - модуль числа Т.
Полагаем P=1
Для всех i от 1 до N-1 при условии что Q=true вычисляем:
1. x_i,y_i
2. x_i+1,y_i+1
3. R=x_i*y_i+1-x_i+1*y_i
4. P=P*Z*R/|R|, здесь |R| - модуль числа R.
5. если P<0, то Q=false
Если Q=true - многоугольник выпуклый, иначе - нет.

Вычисление координат вектора, образованного сторонами многоугольника (x_i, y_i), хорошо производить в отдельной процедуре.
x_i=P^x_i+1-P^x_i
y_i=P^y_i+1-P^y_i
Для N-ой вершины N+1-ая будет, естественно, первой.

const N=8;
type point=record
       x,y:real;
       end;
var Peaks:array[1..N] of point;
    i:byte;
    Q:boolean;
    T,Z,P:real;
    x1,y1,x2,y2:real;
    v1,v2:point;
function Sign(r:real):shortint;
const eps=0.0000001;
  begin
  if (abs(r)<eps) then Sign:=1
  else Sign:=Round(r/abs(r));
  end;
Procedure GetVector(i:byte;var p:point);
  begin
  if (i=N) then
    begin
    p.x:=Peaks[1].x-Peaks[N].x;
    p.y:=Peaks[1].y-Peaks[N].y;
    end
  else
    begin
    p.x:=Peaks[i+1].x-Peaks[i].x;
    p.y:=Peaks[i+1].y-Peaks[i].y;
    end;
  end;
begin
Peaks[1].x:= 0; Peaks[1].y:= 6;
Peaks[2].x:=-4; Peaks[2].y:= 5;
Peaks[3].x:=-5; Peaks[3].y:= 2;
{Peaks[3].x:=-1; Peaks[3].y:= 1; { невыпуклый }
Peaks[4].x:=-5; Peaks[4].y:=-1;
Peaks[5].x:=-2; Peaks[5].y:=-4;
Peaks[6].x:= 4; Peaks[6].y:=-3;
Peaks[7].x:= 6; Peaks[7].y:= 1;
Peaks[8].x:= 4; Peaks[8].y:= 5;
{Peaks[8].x:= 1; Peaks[8].y:= 1; { невыпуклый }

GetVector(N,v1);
GetVector(1,v2);
T:=v1.x*v2.y-v2.x*v1.y;
Z:=Sign(T);
P:=1.0;
i:=1;
Q:=true;
while (Q and (i<N)) do
  begin
  GetVector(i,v1);
  GetVector(i+1,v2);
  T:=v1.x*v2.y-v2.x*v1.y;
  P:=P*Z*Sign(T);
  writeln('i=',i,'; T=',T,'; P=',P);
  if (P<0) then Q:=false;
  inc(i);
  end;
if Q
  then writeln('Многоугольник выпуклый.')
  else writeln('Многоугольник невыпуклый.');
end.